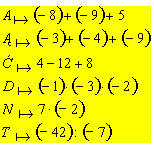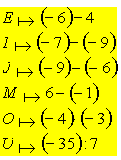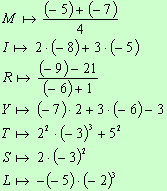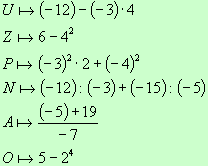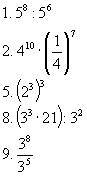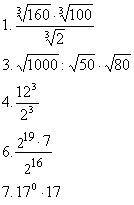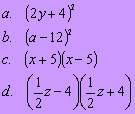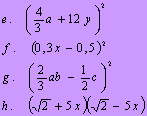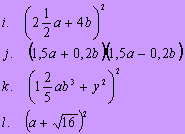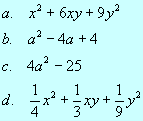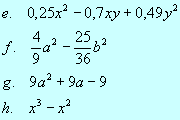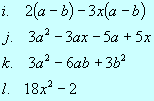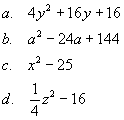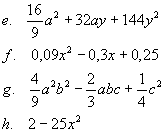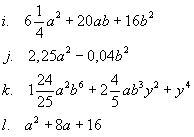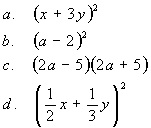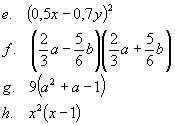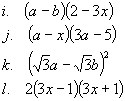Sprawdź, czy i Ty

możesz

zostać Pitagorasem.

I. DZIAŁANIA W ZBIORZE LICZB WYMIERNYCH.

1. Uzupełnij grafy:

a.

b.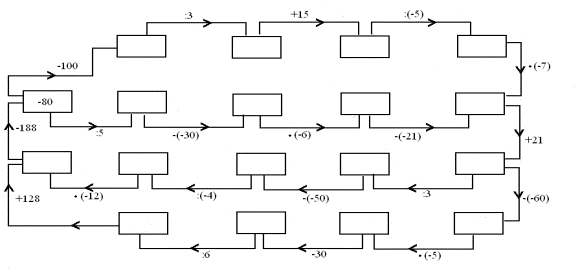

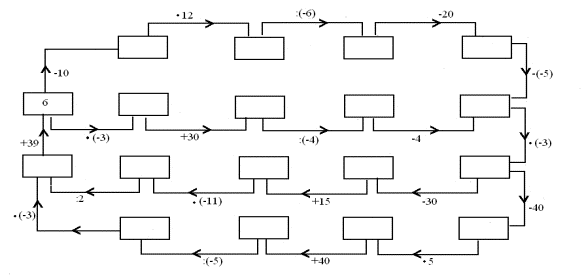
c.

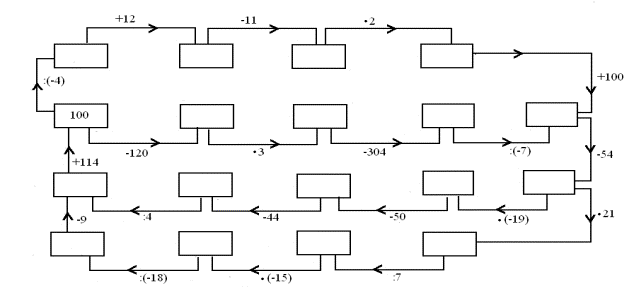
2. Rozwiąż krzyżówki:

		a
	b
c			d	e
		f
	g
h				i
j			k
	l	m

a. poziomo:

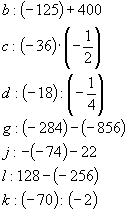
pionowo:

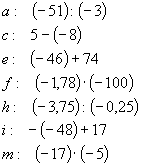
b. poziomo:

	a	b
c				d
			f
		g
	h

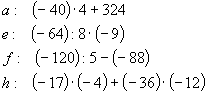
pionowo:

b : 135 – (-18) ^. (-4)

c : 125 : (-5) – (-204)

d : (-56) ^. (- 5) : 2

g : (-23) ^. (-7) – (-3) ^. (-27)

3. Oblicz i odczytaj hasło:

a.

12	-6	-3	-16	0		-5	-3	-10	7	-14	-16
6	12		-6	12	-6	-12	0
-6	12	-6	-12	6	-14	2	-16

b.

-3	-31	7	0	18	6	-2	-10	-35
-3	-31	7	0	18	-83	-11
34	-40	0	18

Odpowiedzi:

1. a.

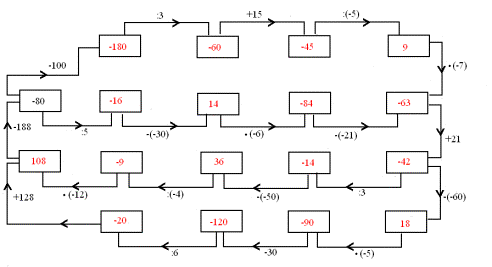
b.

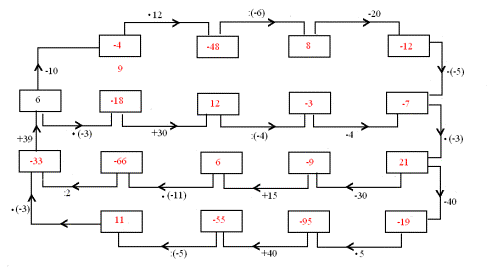
c.

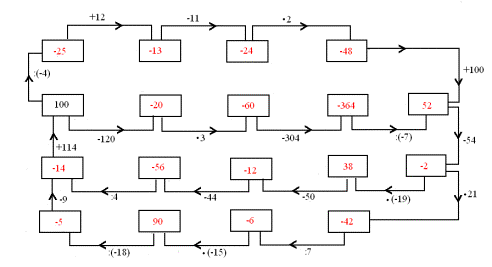
2. a. poziomo: b: 275, c: 18, d: 72, g: 572, j: 52, l: 384, k: 35

pionowo: a: 17, c: 13, e: 28, f: 178, h: 15, i: 65, m: 85

b. poziomo: a: 164, e: 72, f: 64, h: 500

pionowo: b: 63, c: 179, d: 140, g: 90

3. a. hasło: ODJĄĆ UJEMNĄ TO DODAĆ DODATNIĄ

b. hasło: MINUS RAZY MINUS TO PLUS

II. POTĘGI I PIERWIASTKI.

1. Uporządkuj liczby od najmniejszej do największej

a.

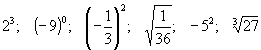
b.

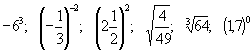
c.

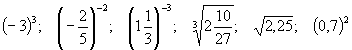
2. Rozwiąż krzyżówkę

poziomo:

pionowo:

1			2	3
		4
	5
6				7
8			8

3. Oblicz i odczytaj hasło:

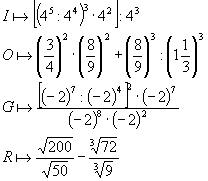
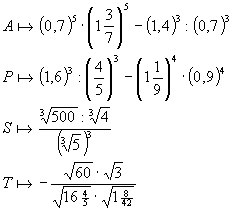
7

16

3

-7

-8

0

-7

1

4. Wyłącz czynnik przed znak pierwiastka:

5. Włącz czynnik pod znak pierwiastka:

Odpowiedzi:

1 a.

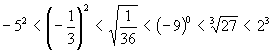
1 b.

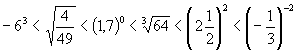
1 c.

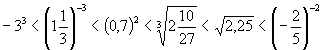
2.

poziomo: 1. 25 2. 64 5. 512 8. 63 9. 27

pionowo: 1. 20 3. 40 4. 216 6. 56 7. 17

3. Hasło: PITAGORAS

4.

5. a. b. c. d.

III. WYRAŻENIA ALGEBRAICZNE.

1. Przekształć następujące wyrażenia na sumy:

2. Oblicz w pamięci:

3. Sprowadź dane wyrażenia do najprostszej postaci (jeżeli trzeba), oblicz ich wartość liczbową dla podanych zmiennych liczbowych i odczytaj hasło:

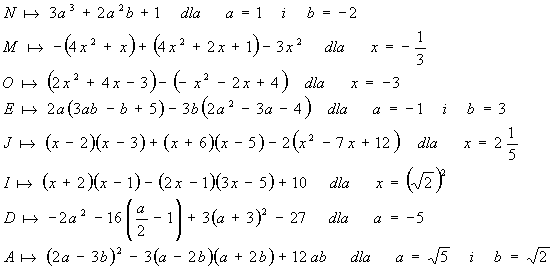
-26

5

-9

0

2

11

47

0

4. Rozłóż podane sumy na czynniki:

Odpowiedzi:

1.

2. a. 196; b. 10021; c. 89996;

3. Hasło: JEDNOMIAN

4.

IV. FUNKCJE I ICH WŁASNOŚCI.

1. Które z przedstawionych przyporządkowań nie jest funkcją określoną na zbiorze X

o wartościach w zbiorze Y i dlaczego?

a. b.

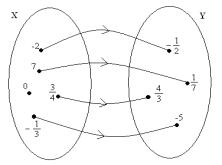
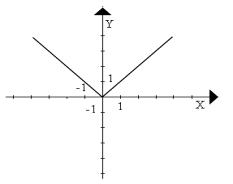
c. d.

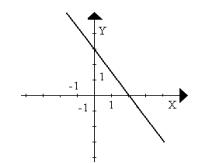
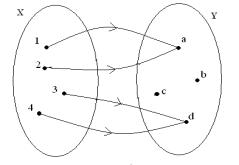
e. f.

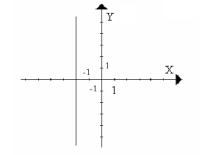
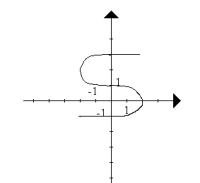
g. każdej liczbie naturalnej x większej od 5 przyporządkowano jej dzielnik ze zbioru Y

2. Podaj dziedzinę i zbiór wartości przedstawionych niżej funkcji:

a. b.

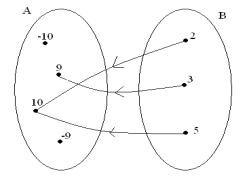
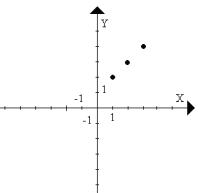
c.

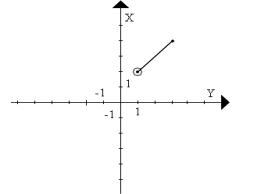
d. y = -x + 3 na zbiorze

e. f.

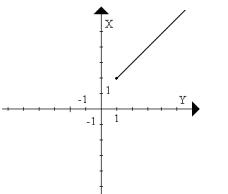
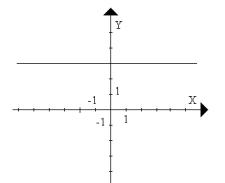
3. Na rysunku przedstawiono wykresy różnych funkcji liniowych. Podaj wzór każdej z nich.

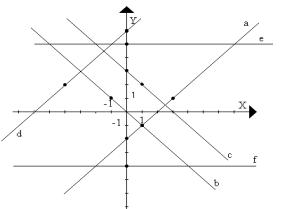
4. Podaj miejsce zerowe funkcji:

a.

b.

x	-7	-5	-2	1	0
y	-2	-3	0	3	2

5. Spośród podanych funkcji wypisz oddzielnie funkcje rosnące, funkcje malejące, funkcje stałe:

6. Sprawdź rachunkowo, czy punkt W należy do wykresu funkcji, gdy:

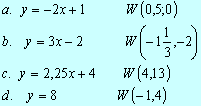
7. Dla jakich argumentów podane funkcje przyjmują wartości dodatnie:

8. Dla jakich argumentów podane funkcje przyjmują wartości mniejsze od -5:

9. Oblicz wartości każdej z podanych funkcji dla argumentu – 1,75:

10. Napisz wzór funkcji, której wykres przechodzi przez punkt P i jest równoległy do wykresu podanej funkcji, gdy:

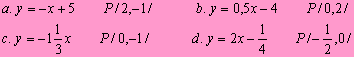
Odpowiedzi:

1. a bo liczbie 0 ze zbioru X nie przyporządkowano ani jednej liczby ze zbioru Y,

e bo liczbie -2 ze zbioru X przyporządkowano nieskończenie wiele liczb ze zbioru Y,

f bo w zbiorze X są liczby, którym przyporządkowano więcej niż jedna liczbę ze zbioru Y,

g bo każda liczba naturalna większa od 5 ma więcej niż jeden dzielnik.

2.

	dziedzina	zbiór wartości
a.
b.
c.
d.
e.
f.

3.

4. a. argument b. argument

5. rosnące:

malejące:

stałe:

6. a. tak, b. nie, c. tak, d. nie

7. a. dla x < 2, b. dla x < 0, c. dla x > 3

8. a. dla x < -1, b. dla x < -2, c. dla x >4

9. a. f(- 1,75) = 9, b. f(- 1,75) = -6,5 c. f(- 1,75) = 14

10. a. y = -x + 1, b. y = 0,5x + 2, c. y = -1x - 1, d. y = 2x +1

V. FIGURY GEOMETRYCZNE.

1. Które ze zdań jest prawdziwe:

A. równoległobok jest prostokątem

B. miara kąta zewnętrznego trójkąta jest równa sumie miar kątów wewnętrznych do niego nieprzyległych

C. kąt wpisany w koło oparty na średnicy ma miarę 180^o

2. Kąt wpisany w koło oparty na okręgu ma miarę:

3. Średnica koła, którego pole jest równe ma długość:

4. Środek okręgu wpisanego w dowolny trójkąt to punkt przecięcia:

A. symetralnych przynajmniej dwóch boków trójkąta

B. wysokości trójkąta

C. dwusiecznych przynajmniej dwóch kątów trójkąta

5. Nie można wpisać okręgu w:

A. prostokąt

B. trójkąt rozwartokątny

C. sześciokąt foremny

6. Środek okręgu wpisanego i opisanego pokrywają się w trójkącie:

A. równoramiennym B. prostokątnym C. równobocznym

7. Promień okręgu opisanego na trójkącie prostokątnym o przeciwprostokątnej i przyprostokątnej ma długość:

8. Wielokątem foremnym jest:

A. romb B. kwadrat C. równoległobok

9. Miara kąta wewnętrznego 12-kąta foremnego jest równa:

10. Które zdanie nie jest prawdziwe?

A. Suma miar kątów wewnętrznych w każdym czworokącie wynosi .

B. Wysokość trójkąta to odcinek łączący wierzchołek trójkąta z przeciwległym bokiem.

C. Styczna do okręgu to prosta, która ma z okręgiem jeden punkt wspólny.

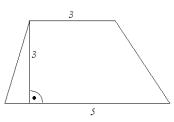
11. Pole rombu jest od pola trapezu:

A. dwa razy większe

B. cztery razy większe

C. równe polu trapezu

12. Liczba przekątnych w 20-kącie foremnym jest równa :

A. 180 B. 170 C. 340

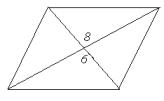
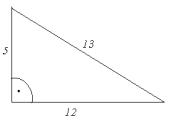
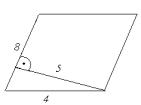
13. Pole równoległoboku jest od pola trójkąta:

A. mniejsze o 20 j ²

B. większe o 10 j ²

C. większe o 7,5 j ²

14. Trójkąt równoboczny i kwadrat mają równe obwody: 120 mm. Która z figur ma większe pole

i o ile cm ² ?

Odpowiedzi:

1. B, 2. C, 3. B, 4. C, 5. A, 6. C, 7. C. 8. B, 9. C, 10. B, 11. A, 12. B, 13. B,

14. kwadrat ma pole większe o 2 cm²

VI. ZASTOSOWANIA TWIERDZENIA PITAGORASA.

1.

a. b.

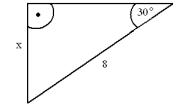
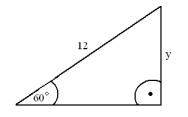
2. Wysokość trójkąta równobocznego o boku jest równa:

3. Promień okręgu opisanego na trójkącie równobocznym o wysokości jest równy:

4. Długość boku trójkąta równobocznego o wysokości jest równa:

5. Długość boku kwadratu o przekątnej jest równa:

6. Długościami boków trójkąta prostokątnego są liczby:

7. Promień okręgu wpisanego w trójkąt równoboczny o boku jest równy:

8. Długość promienia okręgu opisanego na kwadracie o boku jest równy:

9. Przekątna prostokąta o bokach długości ma długość:

10. Zbuduj odcinek, którego długość przy obranej jednostce jest równa .

Odpowiedzi:

1a. C, 1b. B, 2. B, 3. A, 4. B, 5. C, 6. A, 7. C, 8. B, 9. C,

10. szukany odcinek to suma: wysokości trójkąta równobocznego o boku długości 2 i przekątnej

kwadratu o boku długości 1.

„ SPRAWDŹ, CZY I TY MOŻESZ ZOSTAĆ PITAGORASEM’’.

I.DZIAŁANIA W ZBIORZE LICZB WYMIERNYCH.

II.POTĘGI I PIERWIASTKI.

III.WYRAŻENIA ALGEBRAICZNE.

IV.FUNKCJE I ICH WŁASNOŚCI.

V.FIGURY GEOMETRYCZNE.

VI.ZASTOSOWANIA TWIERDZENIA PITAGORASA.